
|
zpět na obsah |
Black-Scholes Model |



Základní myšlenkou modelu je, že cena opce je implictně dána vývojem ceny podkladového aktiva, pro konstrukční jednoduchost modelu se model zpravidla vysvětluje na likvidní akciích.
Model byl sestrojen ekonomy Blackem Fischerem a Myronem Scholesem a publikován v roce 1973. Tito pánové při sestrojování modelu stavěli na dřívějším výzkumu Edwarda O. Thorpa, Paula Samuelsona a Roberta C. Mertona. Merton a Scholes získali v roce 1997 za tento model a související práci nobelovu cenu v oblasti ekonomie. Black se Nobelovy ceny bohužel nedožil, zemřel v roce 1995.
Základní předpoklady modelu:
Pro pochopení a správnou funkčnost tohoto modelu je nutné brát zřetel na jeho předpoklady. Black-Scholes model je relativně složitou konstrukcí a neznalost jeho předpokladů může vést k chybám při jeho použití.
- Cena podkladového aktiva se vyvíjí podle geometrického brownova pohybu (speciální typ stochastického procesu) s konstantním posunem (odchylkou) a konstantní volatilitou. Předpoklad konstantní volatility je velice důležitý, je nutné si uvědomit, že volatilita aktiv se na trzích mění. Nutno upozornit nejen na to, že volatilita akcií se mění v čase, ale obzvláště důležitý fakt je i změna korelace aktiv. V období stresu volatilita na akciových trzích roste a prudce se zvyšuje i korelace mezi aktivy.
- Obchodování s podkladovým aktivem je kontinuální, v přeneseném smyslu likvidní. Cenu podkladového aktiva je možné stanovit v každém okamžiku. Toto je důvod, proč ocenění opce přes Black-Scholes model je nutné doplnit i o další nástroje pokud oceňujeme méně likvidní aktiva, například over-the-counter (OTC) instrumenty.
- Neexistují transakční náklady a daně.
- Zapůjčení hotovosti je možné za konstantní bezrizikovou úrokovou míru.
- Všechna aktiva jsou perfektně dělitelná (není problém koupit například 1/100 akcie).
- Na trhu neexistují příležitosti pro arbitráž. Toto je spíše technický předpoklad modelu.
- Technicky je možné podkladové aktivum prodat se záměrem pozdější koupě (short sell).
Praktickým výsledkem a težištěm Black-Scholesova modelu je následující rovnice:
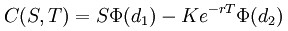
kde
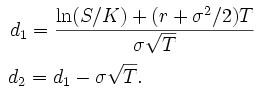
C(S,T) nám říká, že se jedná o rovnici ocenění evropské kupní (call) opce (opce splatná pouze v čase T, nelze ji uplatnit před dobou splatnosti), přičemž K je cena dodání akcie v současnosti oceněné jako S. Jinými slovy, rovnice oceňuje právo koupit akcii za cenu K v čase T. R je konstantní úroková míra a písmenko σ (delta) je volatilita (konstanta).
Výpočtem hodnot d1 a d2 se dostaneme k parametrům rovnice. Písmenko Φ (phi) představuje kumulativní distribuční funkci standardního normálního rozdělení. Kumulativní distribuční funkce standardního normálního rozdělení je tabularizovaná hodnota, zjednodušeně řečeno, parametru d odpovídá jakási hodnota Φ, která je vyjádřením kumulativní pravděpodobnosti v normálním rozdělení.
Cena put opce (právo prodat akcii za cenu K v čase T) se vypočte převodem přes put-call paritu, a to jako:
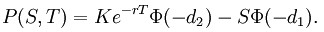
Výhodou Black-Scholesova modelu je jeho výpočtová nenáročnost a celosvětová rozšířenost. Provede se pár odhadů vstupních hodnot, vynásobí se pár čísel, najdou se hodnoty ve statistických tabulkách a máme cenu opce. Tento model je známý v celosvětové finanční praxi a opravdu se používá. Úskalí modelu je v použití správných vstupních dat. Podíváme-li se na předpoklady modelu, je jasné, že většina z nich je v opravdovém světě reálná jen omezeně. Nejen, že v reálném světě existují daně a transakční náklady, ale i další větší komplikace. Už jsme zmínili, že volatilita se mění v čase.
Volatilita je navíc proměnná i v závislosti na použitém podkladovém aktivu a na době splatnosti. Akcie jsou charakterizovány deformovanou křivkou volatility s negativním sklonem. Implikovaná (trhem očekávaná, domnělá) volatilita je vyšší u opcí vypsaných na akcie s nižšími dodacími cenami (strike price) a nižší pro opce s vyššími dodacími cenami (přestože mluvíme o totožném podkladovém aktivu, pouze dodací cena tvoří rozdíl ve volatilitě).
Světové měny mají křivku volatility více symetrickou než akcie. Opce v penězích (at-the-money) vypsané na měnu mají implikovanou volatilitu nejnižší zatímco opce v penězích (in-the-money) a mimo peníze (out-the-money) vykazují implikovanou volatilitu vyšší.
Komodity se vyznačují inverzním vztahem vůči akciím. Implikovaná volatilita u komoditních opcí je nejvyšší u vysokých dodacích cen a nejnižší u nízkých dodacích cen.
Základní Black-Scholes model nelze přímo aplikovat na dluhopisy, protože porušují předpoklad stochastického procesu vývoje cen i předpoklad konstantní volatility. Dluhopisy jsou charakterizovány takzvaným pull-to-par efektem. Jak se dluhopis blíží k době splatnosti, všechny ceny spojené s dluhopisem jsou známy se vzrůstající jistotou, což snižuje volatilitu. Oceňování opcí na dluhopisy se věnují rozšířené verze Black-Scholesova modelu.
V praxi je použití základní Black-Scholesovy rovnice ještě o něco složitější. Pokud podkladové aktivum vyplácí dividendy nebo jsou s jeho držbou spojeny náklady, je nutné použít rozšířenou verzi Black-Scholesova modelu. Základní verze rovněž předpokládá vypsání evropské opce (opce splatné pouze v době splatnosti). Americká opce (splatná klikoliv do doby splatnosti) vnáší do modelu další komplikace.
Black-Scholes Model
Související pojmy
Související pojmy
Diskuzní fórum / komentáře
Dukiszín fmóur / kteoeřnám
Další zdroje informací
Další zdroje informací
|
Co by Vás ještě tak asi mohlo zajímat?
Co by Vás ještě tak asi mohlo zajímat?
Nejsledovanější knihy
Nejsledovanější knihy
Ekonomie
Holman Robert
Holman Robert
(Sledovanost: 175)
Marketing
Boučková Jana, a kol.
Boučková Jana, a kol.
(Sledovanost: 169)
Introduction to Financial Accounting
Charles T. Horngren, Gary L. Sundem, John A. Elliott, Donna Philbrick
Charles T. Horngren, Gary L. Sundem, John A. Elliott, Donna Philbrick
(Sledovanost: 168)
Corporate Finance
Stephen A. Ross, Randolph W Westerfield, Jeffrey Jaffe
Stephen A. Ross, Randolph W Westerfield, Jeffrey Jaffe
(Sledovanost: 162)
Financial Accounting : Introduction to Concepts, Methods and Uses
Clyde P. Stickney, Roman L. Weil
Clyde P. Stickney, Roman L. Weil
(Sledovanost: 162)
Diskuzní fórum
Středoevropské centrum pro finance a management podporuje veřejnou diskuzi týkající se různých ekonomických i společenských témat.
Diskuze na těchto stránkách je neredigovaná a nemoderovaná. V zájmu zachování vysoké úrovně diskuze i tohoto servru je však administrátor fóra oprávněn konat patřičné kroky, aby bylo zabráněno projevům rasové, národnostní, náboženské nebo jinak nepřípustné diskriminace. Administrátor je rovněž oprávněn zasahovat, pokud objeví v diskuzích vulgární nebo jinak nepřístojné projevy.
Středoevropské centrum pro finance a management nenese žádnou faktickou ani implicitní odpovědnost za obsah jednotlivých příspěvků, ani neručí za skutečnou identitu jejich autorů.
V zájmu udržení vysoké úrovně diskuzí žádáme autory, aby identifikovali své příspěvky svým jménem nebo alespoň přezdívkou a pokud možno i elektronickou adresou.
Děkujeme za přízeň a doufáme, že naše www stránky nabízejí co hledáte.
Středoevropské centrum pro finance a management
Svět plný ověřené vzdělanosti
Dnešní datum:
| leadership - management | strategie - rozhodovací procesy | organizace - změna - kultůra | komunikace - marketing |
| přístupy & metody A-Z | systémy & teorie A-Z | modely & struktůry A-Z | metody & způsoby A-Z |
| oceňování - rozhodování | strategie - tvorba hodnot | treasury - cash flow | finance - řízení rizik |
| metody & ukazatele A-Z | modely & způsoby A-Z | přístupy & systémy A-Z | metody & teorie A-Z |
Upozornění
Upozornění na novou službu: Právě jsme spustili Katalog odborníků, konzultantů a profesionálů. Odkaz Odborníci.
Vyhledávání
Novinky
Sharpe Ratio
Treynor Ratio
Sortino Ratio
Crashophobia
Portfolio Turnover Ratio (PTR)
Opce - delta hedging
Black-Scholes Model
Treynor Ratio
Sortino Ratio
Crashophobia
Portfolio Turnover Ratio (PTR)
Opce - delta hedging
Black-Scholes Model
Vybrané finanční a manažerské okruhy na webu
Dnes Vám představujeme
Ing. Lukáš Svoboda
consultant SAP ERP v oblasti financí -- Působím jako SAP konzultant v oblasti financí (účetnictví, majetek, rozpočetnictví) ve společnosti KCT Data, která se orientuje zejména na produkty a technologie SAP. Ve společnosti pracuju od roku 2003.
Více se dozvíte zde.
Více se dozvíte zde.
Anketa
Nejčtenější pojmy
z financí a managementu
z financí a managementu
SWOT analýza
SWOT je typ strategické analýzy stavu firmy, podniku či orga...
(Přečteno: 144668x)
Zrušení, likvidace, zánik společnosti
Zrušení a zánik společnosti se řídí v České republice zákonem 51...
(Přečteno: 130270x)
Definice cíle SMART (Project Management)
SMART je souhrn pravidel, která pomáhají především v r...
(Přečteno: 107886x)
Lorenzova křivka
Lorenzova křivka, nebo anglicky Lorenz Curve (LC), je grafické znáz...
(Přečteno: 79530x)
Giniho koeficient
Giniho koeficient, sestrojený italským statistikem Coradem Gini v r...
(Přečteno: 77514x)
Upozornění
Spolupráce: Napsali jste kvalitní odbornou práci, studii nebo analýzu, která Vám nyní leží v šuplíku? Publikujte ji na tomto portálu. Co Vám za to můžeme nabídnout najdete na stránce informace pro autory.
Další kategorie
